Special Relativity

The special theory of relativity deals with motion, mass, and energy in modern physics. It fixes the cracks in Newtonian physics that started to show in Maxwell’s Equations. Special Relativity is a subset of the general theory of relativity and does not incorporate acceleration and gravity.

The Clash Between Newtonian Physics and Maxwell’s Equation.

Remember that the speed of light is approximately equal to $\frac{1}{\sqrt{{\mu }_0{ϵ}_0}}$. However, this fundamentally breaks Newton’s laws. Newton’s laws are relative, meaning that they depend on the frame of observation. However, Maxwell’s equations predict that the speed of light should be constant no matter what and regardless of reference frame.

Einstein’s Postulates of Relativity

1. The Principle of Relativity - The laws of physics take the same form in all inertial frames of reference.
2. Invariance of $c$ - The speed of light in free space has the same value in all inertial frames of reference.

4D Spacetime

Instead of evaluating space as a 3-dimensional space, Einstein proposed that we use a 4 dimensional vector.

ct \\ x \\ y \\ z \end{pmatrix} = \begin{pmatrix} ct \\ \vec{r} \end{pmatrix}

If you notice, we use $ct$ as our 4th dimension. This allows us to use time as an additional reference, but we make the units compatible with the other values by multiplying by c, which is always constant everywhere in space.

Minkowski Spacetime:

$(\Delta r{)}^2=-(c\Delta t{)}^2=(\Delta x{)}^2+(\Delta y{)}^2+(\Delta z{)}^2$ This equation allows us to predict the speed of light. No matter what we are doing, and where in physics, this equation should always yield the speed of light! This is super important because it standardizes the interpretation of universal phenomenon between two different observers. 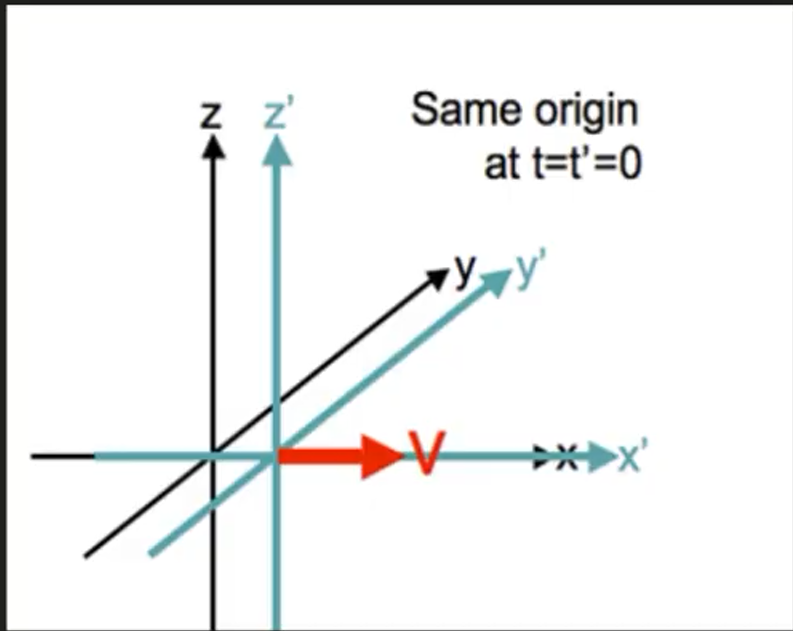Let us consider the image above. In this image, the frame of reference $r^{\prime }$ is moving relative to the initial frame of reference $r$. This can be described by the Lorentz Transformation for this situation. $r^{\prime }=\left(\begin{array}{c}c{t}^{\prime }=\gamma (ct-\frac{vx}{c})\\ x^{\prime }=\gamma (x-vt)\\ y^{\prime }=y\\ z^{\prime }=z\end{array}\right)$ where $\gamma$, the gamma factor is defined as: $\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}$

Relativistic Velocity Addition Formula

All of these result in a new formula for relative velocity: ${\mu }_x=\frac{{\mu }_x^{\prime }+v}{1+\left(\frac{v{\mu }_x^{\prime }}{c^2}\right)}$ Lets examine what happens when we have a stationary observer observing someone moving at the speed of light, firing a laser moving at the speed of light! If we plug in ${\mu }^{\prime }=c$ and $v=c$, we will find that the answer is still c!! The speed of light is invariant and is proven by Einstein’s equations.

Time Dilation and Length Contraction:

Time and length in relativity are not constant! Because of relativistic effects that occur at speeds comparable to the speed of light, time and length can vary from observer to observer.

The Lorentz transformation says that time differs in the following way: $\Delta t=\gamma (\Delta t^{\prime }+\frac{v\Delta x^{\prime }}{c^2})$ To measure time, we measure $\Delta t^{\prime }$, when $\Delta x^{\prime }=0$! This yields the following formula: $\Delta t=\gamma \Delta \tau$ In the above equation, $\Delta \tau$(the proper time), is the time measured by the moving observer (the time measured by a clock with the same motion as the observer). $\Delta t$ is the time seen by the outside observer (outside frame).

Relativity similarly modifies distances! The equation for length contraction is given by: $\Delta x=\frac{\Delta \rho }{\gamma }$ where $\Delta \rho$ is the proper length. The proper length is the length measured by an observer that’s at rest relative to it.

3 Dimensional Proper Velocity:

$\vec{\nu }=\frac{dr}{d\tau }=\gamma \frac{d\vec{r}}{dt}=\gamma \vec{v}$ We get this equation by recognizing that $t=\tau \gamma$, and deriving. We initially derive by $\tau$ because that’s the universally agreed upon time for all observers.

NOTE: Nu represents the PROPER TIME and v represents our measured time.

Note the invariant property for squaring the magnitude of the proper velocity. No matter who you are, this property holds true.

Momentum

Momentum in relativity can now be constructed because we have both mass (no different than normal) and velocity in relativity. The formula comes from simply substituting $\vec{v}$ with $\vec{\nu }$. $\vec{p}=m\vec{\nu }=\gamma m\vec{v}$ Note how the energy(shown in next section) is part of the time component of the momentum 4 vector!

If you take the magnitude of the momentum squared, you get the following expression: 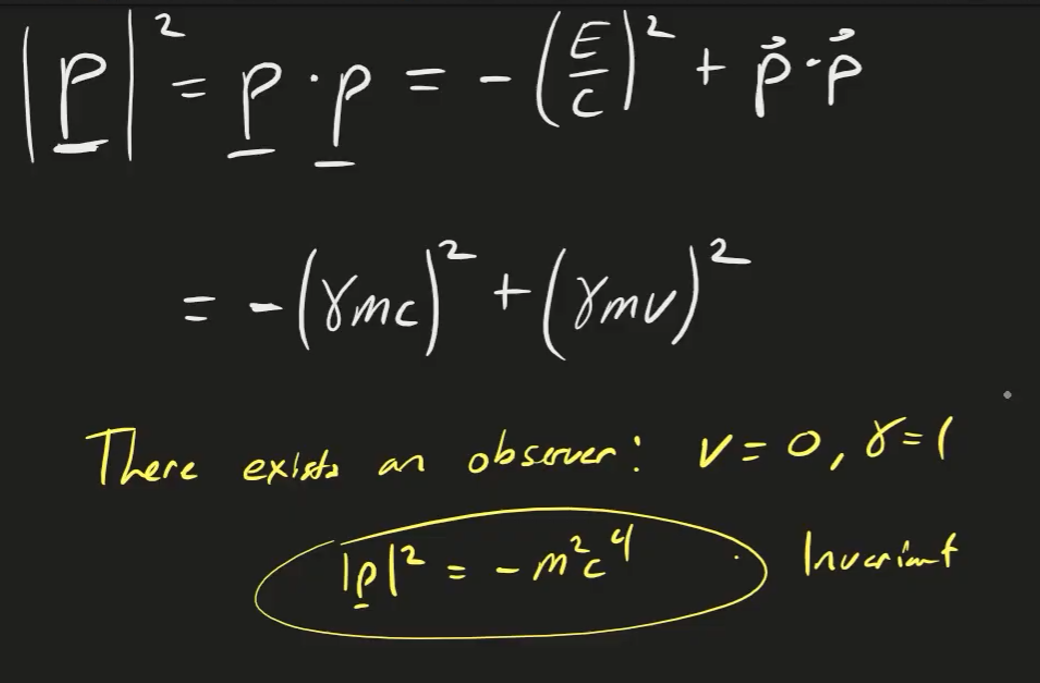This means that every single observer must conclude the the magnitude of the momentum squared must be equal to $-m^2{c}^2$. We can take this a step further and conclude: 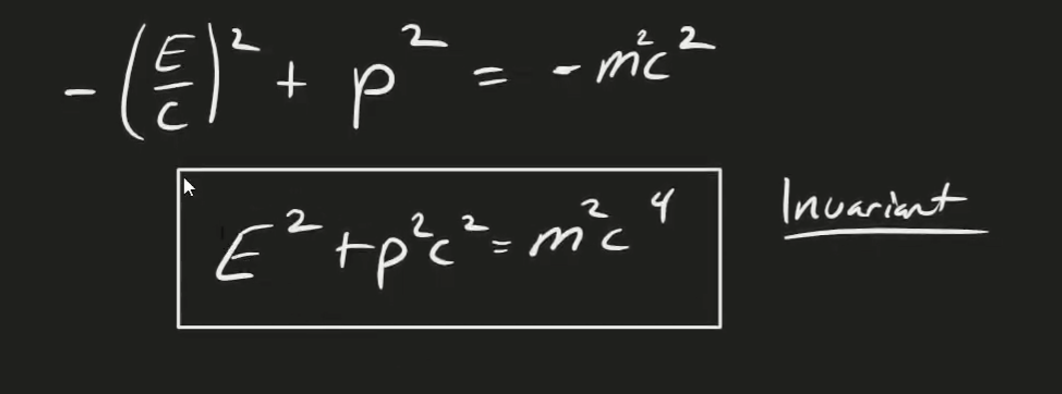This means that momentum and energy are inherently coupled to a single value!!!!

Summary:

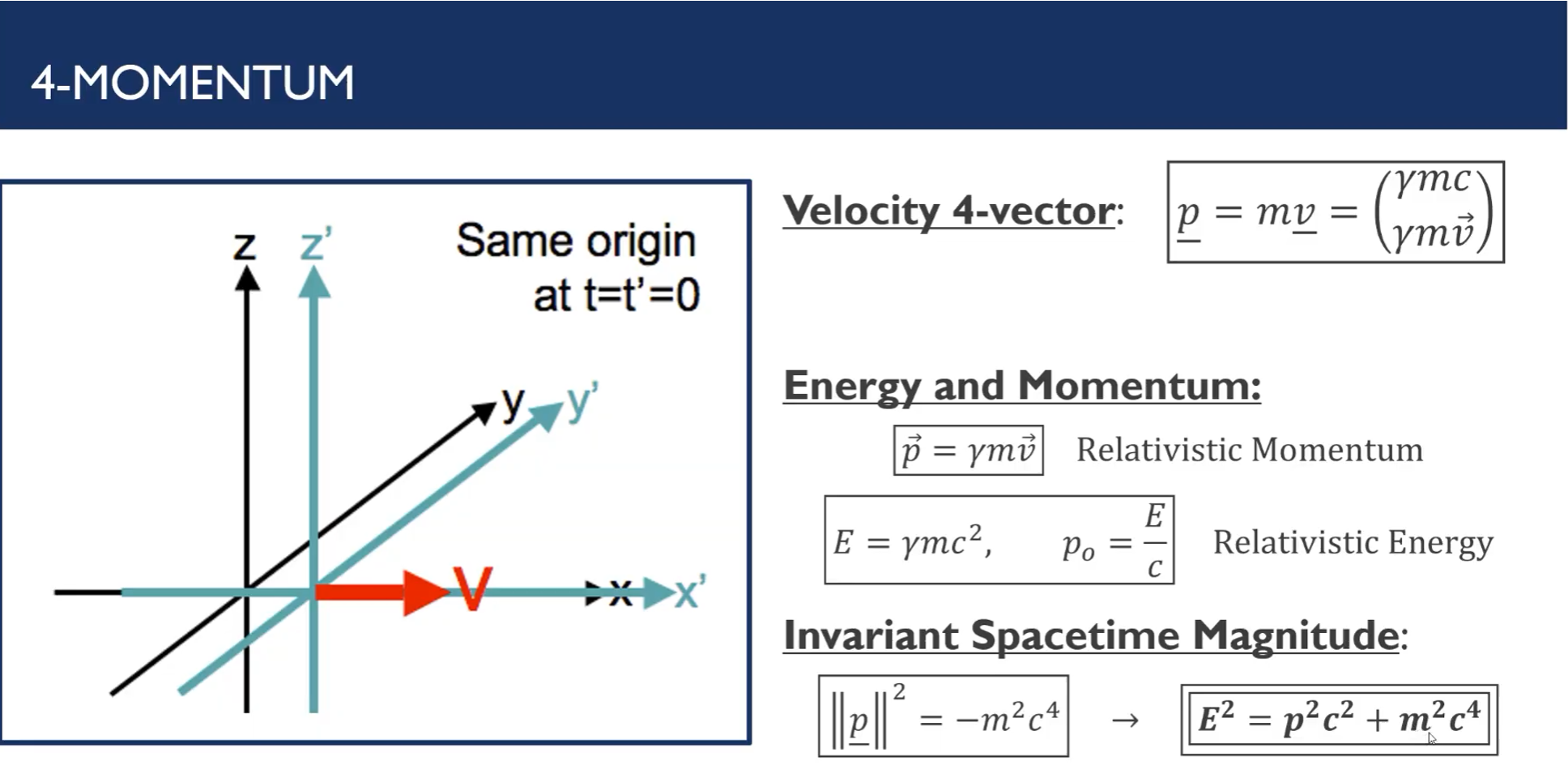From the invariant spacetime magnitude we can extract two further famous subcases:

1. If m = 0: $\frac{E}{c}=p$
2. If p = 0: $E=m{c}^2$ The famous result $E=m{c}^2$ is known as the rest energy of a system! All other systems in motion are given by the full equation for the invariant spacetime magnitude. This result is huge, because it asserts that the energy of a system isn’t lost when it’s at rest, but is instead stored in its mass!

Relativistic Energy

$E=\gamma m{c}^2$

Kinetic Energy

Remember that $m{c}^2$ is the rest energy, so subtracting from total energy gives the energy due to movement. $KE=E-m{c}^2$ We then substitute for $E$: $KE=\gamma m{c}^2-m{c}^2$ Simplifying further: $KE=(\gamma -1)m{c}^2$

Force

Remember that force is simply: $F=\frac{d\rho }{d\tau }$

NOTE: You MUST derive by the PROPER TIME!!!