Electromagnetic Waves

Background

Maxwell’s Equations are critical to setting up the idea of the electromagnetic wave. In a vacuum, terms of Maxwell’s equations cancel, but some still persist! The equations in a vacuum become: $\nabla \times \vec{E}=-\frac{d\vec{B}}{dt}$ and $\nabla \times \vec{B}={\mu }_0{ϵ}_0\frac{d\vec{E}}{dt}$ with the other equations simply being equal to 0. Thus, we can see that electric and magnetic fields still persist in vacuum. This explains why light and other waves propagate through space!

The Mechanism of EM Wave Propagation:

The image above describes the mechanism by which EM waves propagate in space. An oscillating B field, caused by the current in the wire creates an oscillating E field perpendicular to the B field. This E field creates another oscillating B field, and this process goes on ad infinitum…

NOTE: This ONLY works for OSCILLATING fields. Why? Remember that the electric and magnetic field are time dependent, thus requiring that you derive the function for one to get the other. Because oscillations come in the form of a sin or cos function, they can be derived infinitely. Compare this to a function such as 7x, which only lasts for a single derivative before becoming constant.

Properties of EM Waves

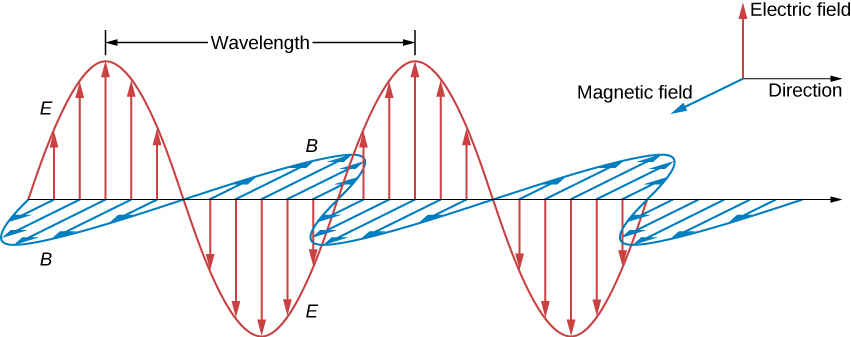The electric and magnetic fields of an EM wave are in phase. This means that when the $\vec{B}$ field is at maximum, so is the $\vec{E}$ field. We can also realize that the $\vec{E}$ field, $\vec{B}$ field, and $\vec{v}$ are always perpendicular.

Manipulating Maxwell’s Equations, we can predict the speed of light and the propagation speed of an EM wave (the same as the speed of light). This speed is: $c=\frac{1}{\sqrt{{\mu }_0{ϵ}_0}}=3\times 10^{8}m/s$ Furthermore, the speed of light can be used to relate the two fields! $\frac{||\vec{E}||}{||\vec{B}||}=c$ EM waves propagate energy and momentum in the direction of wave motion. Because it has momentum, EM waves can exert pressure when absorbed or reflected by other materials.

NOTE: Light is an EM wave, but do note: LIGHT IS MASSLESS, along with all other EM waves! But how can a massless object have a momentum and impart a force? This contradiction between Newton and Maxwell was solved by Einstein and the theory of Special Relativity.

The Mathematic Basis for EM Waves

To keep things simple, we will solely study waves that are sinusoidal. Waves of a fixed frequency are called monochromatic and their equations take the form: $\vec{E}(x,t)=E_{0}cos(kx-\omega t)\hat{y}$ and $\vec{B}(x,t)=B_{0}cos(kx-\omega t)\hat{z}$ Do not forget these basic equations: $k=\frac{2\pi }{\lambda },\omega =2\pi f,c=\frac{\omega }{k}=\lambda f$

Energy in EM Waves:

From what we know about the Poynting Vector, we can do the following algebra: Thus, we find the the energy stored in the electric and magnetic field are the same. We can also rewrite the Poynting vector as: $\vec{S}(x,t)=c{\mu }_{EM}\hat{z}$ It is often useful to find the average of the Poynting vector, which is: $I=S_{avg}=\frac{c{ϵ}_0{E}^2}{2}$ where $I$ is the intensity. Through algebraic manipulation, we can also produce the equation: $I=\frac{c{B}_0^2}{2{\mu }_0}$ which gives the intensity in terms of the magnetic field! We can further use algebra to find an intensity equation that gives the intensity in terms of both magnetic and electric fields! $I=\frac{E_0{B}_0}{2{\mu }_0}$ Because we are examining sinusoidal waves, we can find the peak intensity with the following equation: $I_0=2I$ Finally, don’t forget that $I$ (intensity) is simply $I=\frac{P}{A}$

Radiation Pressure

For a perfect absorber: $p=I/c$ For a perfect reflector: $p=2I/c$

Momentum in EM Waves

Electromagnetic waves have momentum. One such equation for this is $\vec{p}=\frac{\vec{S}}{c^2}$

Note: p above is the momentum per volume!

From earlier, we can use the alternate equation for the Poynting vector: $\vec{S}=cu\hat{z}$ and substitute to give us: $p_{EM}=\frac{E}{c}$ where E is the energy of the wave.

From this result, we can see that light has momentum! This has the implication that light can exert a force, since it can exchange momentum! Remember that force is: $\vec{F}=\frac{d\vec{p}}{dt}$

Relativity

$E^2=p^2{c}^2+m^2{c}^4$