Biot-Savart Law

The Biot-Savart Law is a very useful law in the calculation of the magnitude and direction of a magnetic field produced by a current in a wire, therefore letting us find Magnetic Forces and Fields. In fact, the Biot-Savart Law is the method by which we derive the formula for the magnetic force produced by a current in a wire. Note that if there is symmetry in the problem between $\vec{B}$ and $\overrightarrow{dl}$, Ampere’s Law may be a better method to use.

At any position $P$, the magnetic field $d\vec{B}$ due to an element $d\vec{l}$ of a current carrying wire is given by: $d\vec{B}=\frac{{\mu }_0}{4\pi }\frac{Id\vec{l}\times \hat{r}}{r^2}$ The constant ${\mu }_0$ is called the permeability of free space and is exactly ${\mu }_0=4\pi \times 10^{-7}T\ast m/A$. The direction of the magnetic field is found using the right hand rule between $d\vec{l}$ and $\hat{r}$.

NOTE: The unit vector for dl points IN THE DIRECTION OF CURRENT! And the vector for r points from the current element towards the point where the field is desired.

Examples and Strategies

Short Current Segments:

For very small current segments in which the radius $r$ is much larger than the $\overrightarrow{dl}$ that we are looking at, we can approximate that the radius, and therefore the magnetic field contribution of each segment $\overrightarrow{dl}$ is approximately the same. This allows us to drop the integral, and change the $\overrightarrow{dl}$ to a $\Delta l$. The equation is then as follows: $B=\frac{{\mu }_0}{4\pi }\frac{I\Delta lsin\theta }{r^2}$

Circular Arcs of Wire:

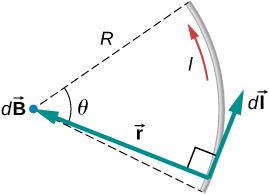There are three key realizations to be able to tackle this problem:

1. Anywhere on the arc, $\overrightarrow{dl}$ and $\vec{r}$ are perpendicular to each other. This means that we can drop the $\sin \theta$ term when expanding the cross product since $\sin (90)=1$.
2. $\vec{r}$ always has the same magnitude, which makes it a constant, and can therefore be pulled out of the integral.
3. $\overrightarrow{dl}$ can be rewritten as $rd\theta$ (This comes from the arclength formula) After substituting these in, we find that the final equation becomes: $B=\frac{{\mu }_{0}I\theta }{4\pi r}$

Thin Straight Wires:

The thin straight wire is a slightly more complicated example than the previous ones. We first refer to the diagram to find a few critical relations.

1. $r=\sqrt{x^2+R^2}$ by the Pythagorean theorem.

2. $\sin \theta =\frac{R}{\sqrt{x^2+R^2}}$ By substituting these relationships into the equation, we can rewrite the integral: $B=\frac{{\mu }_{0}I}{2\pi }{\int }_b^a\frac{Rdx}{(x^2+R^2{)}^{1/2}}$ After integrating, we get: $B=\frac{{\mu }_{0}I}{2\pi R}{\left[\frac{x}{(x^2+R^2{)}^{1/2}}\right]}_b^a$ and after evaluating with respect to $\overrightarrow{dx}$ from 0 to $\infty$, we reach the following very important equation: $B=\frac{{\mu }_{0}I}{2\pi R}$ This equation gives the magnetic field a distance $R$ away from a wire with current $I$.

   NOTE: The direction of the magnetic field is given by the right hand rule. Place your thumb in the direction of the current and curl. The direction your fingers curl indicates the direction the magnetic field goes. Remember that the magnetic field for a wire resembles circles spinning around the wire.

Two Parallel Currents:

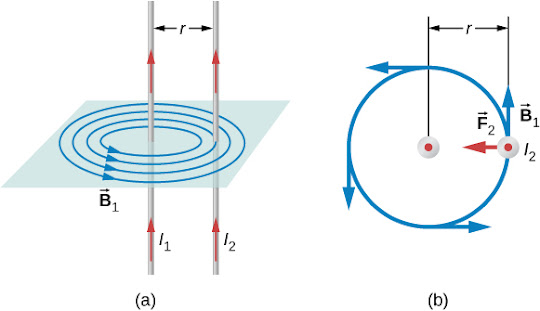Using our knowledge from the thin straight wire, we know that $B_1=\frac{{\mu }_{0}I}{2\pi R}$ We know that the field from wire one is perpendicular to the current in wire two, so the force on wire two is: $F_2=I_{2}l{B}_1$ Both forces and magnetic fields on each wire have equal magnitudes since they carry the same current and they have the same length. Thus, we can drop the subscript and change $F_2$ to simply $F$ (Note:$-F_1=F_2$). Furthermore, we can substitute $B_1$ into the above equation to get a special equation: $\frac{F}{l}=\frac{{\mu }_0{I}_1{I}_2}{2\pi r}$ The ratio of $\frac{F}{l}$ gives us the force per unit length between two parallel currents ($I_1$ and $I_2$) separated by a distance of r.

NOTE: THIS FORCE IS ATTRACTIVE IF BOTH CURRENTS ARE IN THE SAME DIRECTION, AND REPULSIVE IF BOTH ARE IN OPPOSITE DIRECTIONS.

This result is the reason for the pinch effect, where two power lines arc together if too close.

Current Loop:

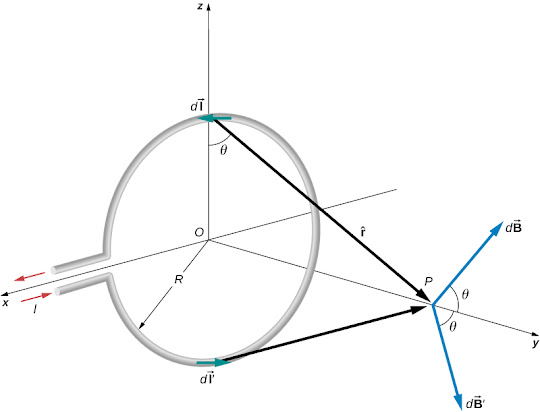Again, we want to make a couple key realizations to solve this problem.

1. Each point on the ring creates a magnetic field whose x component cancels with the x component on the other side of the ring. Thus, there is only a y component.
2. $r=\sqrt{y^2+R^2}$
3. $cos\theta =\frac{R}{\sqrt{y^2+R^2}}$