RLC Circuits

RLC with No Power Supply:

Consider a circuit with all of the following components: A charged capacitor, a resistor, and an inductor, all in series!

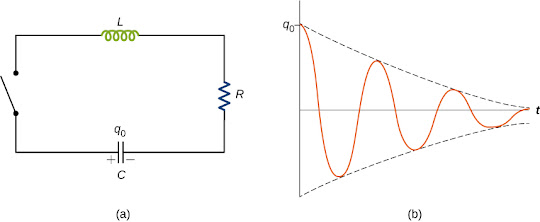
Analysis of this circuit gives a differential equation that can be solved to give the function:

RLC Circuits with AC:

Alternating Current (AC) sources produce a voltage that is variable, usually represented in the form: $v(t)=V_0\sin (\omega t)$ Such an oscillating voltage adds a new complexity to the RLC circuit, but we solve it in a similar fashion to before.

First and foremost, we write the circuit as a combination of voltage drops: $v_R(t)+v_L(t)+v_C(t)=V_0\sin (\omega t)$ We can find the total impedance of this system, and through that, we can find the current in the system. The impedance is given by the following equation: $Z=\sqrt{R^2+(X_L-X_C{)}^2}$ This expression can also be found through Complex Analysis. We then divide the voltage by this quantity, and we can find the current. $I_0=\frac{V_0}{\sqrt{R^2+(X_L-X_C{)}^2}}=\frac{V_0}{Z}$ The impedance is the AC analog to resistance in a DC circuit. The impedance measures the combined effect of resistance, capacitive reactance, and inductive reactance (Units: Ohms).