Magnetic Forces and Fields

The magnetic field is very similar to the Electric Field in that both forces are propagated through space, are action-at-distance forces, and also both usually interact in tangent with each other on the same charged particles. It is critically important to note that the magnetic field DOES NOT DO WORK (The energy in the system doesn’t change).

Note: Because the kinetic energy can never be changed by the magnetic force, we can deduce that the magnetic force can only change the DIRECTION of the particle, not the speed or energy in it.

Magnetic Forces on a Charged Particle

The magnetic field is created by the motion of charged particles, or current. The force on a charged particle by a magnetic field is given by the following equation: $F=q(\vec{v}\times \vec{B})$ It’s very important to note the presence of the cross product, as it implies that the velocity of the charged particle, the magnetic field, and the resulting force are all related by the right hand rule!

NOTE: WHEN USING THE RIGHT HAND RULE, YOU MUST ACCOUNT FOR THE CHARGE OF THE PARTICLE. IF THE PARTICLE IS NEGATIVE, YOU MUST REVERSE THE ORIENTATION GIVEN BY THE RIGHT HAND RULE.

The magnetic field $\vec{B}$ has the SI unit of the Tesla(T). This has the following unit: T = $\frac{N}{A\ast m}$. There is also a smaller unit called the Gauss(G) where $G=10^{-4}T$.

Drawing Magnetic Fields

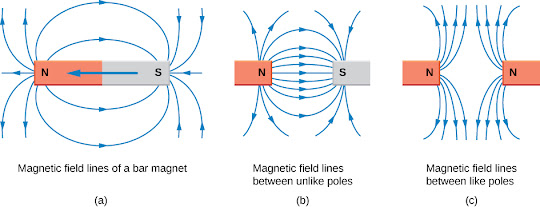
It is also worth noting the way in which we depict magnetic fields and the rules that apply:

1. The direction of the magnetic field is tangent to the field line at any point in space. A small compass will point in the direction of the field line.
2. The strength of the field is proportional to the closeness of the lines. It is exactly proportional to the number of lines per unit area perpendicular to the lines (called the areal density).
3. Magnetic field lines can never cross, meaning that the field is unique at any point in space.
4. Magnetic field lines are continuous, forming closed loops without a beginning or end. They are directed from the north pole to the south pole.

In a wire with a given current, the magnetic field forms a circle as shown below. At each point on the circle, the magnetic field is tangent to the circle. This is shown in the below figure, where we can again see the usefulness of the right-hand rule. You must point your thumb in the direction of the current, and curl your fingers to find the direction of the field lines.

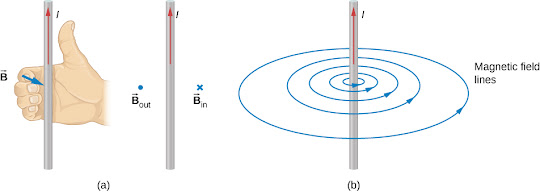
Magnetic Field of a Current-Carrying Wire

We can calculate the magnetic field of a wire carrying a current from the equation above. We first realize that $I=neA{V}_d$. Then, we construct a calculus equation: $d\vec{F}=(nA\ast dl)e\overrightarrow{v_d}\times \vec{B}$. The number of charge carriers in the wire is given by $nA\ast dl$, and the magnetic force that each one of those charge carriers applies is given by: $e\overrightarrow{v_d}\times \vec{B}$. Grouping terms, we find that we can substitute in the equation for the current, simplifying our equation to: $d\vec{F}=I(\overrightarrow{dl}\times \vec{B})$

If the wire happens to be straight, and $\vec{B}$ is uniform, then we simply end up with: $\vec{F}=I\vec{l}\times \vec{B}$

Torque and Magnetic Fields (MOTORS)

The magnetic field is heavily leveraged to create motors! In this application, a loop of wire is placed between two poles of a magnet. When current runs through the wire, it creates a torque on the wire loop, spinning the motor. 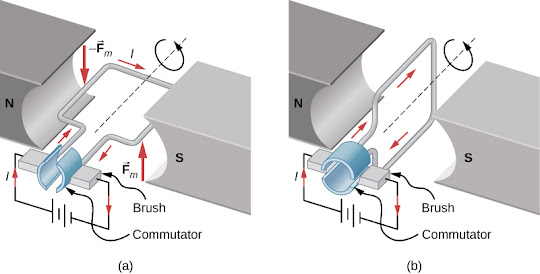To find the net force on any such loop, one has to consider all sides and calculate the torque. Remember that torque is transmitted through a moment arm, so the length of the moment arm MUST BE CONSIDERED.

NOTE: There is NO NET FORCE (BUT THERE IS TORQUE) on a current loop in a uniform magnetic field!

For any closed current loop, you can find the torque on the loop with the formula: $\vec{\tau }=-IABsin\theta \hat{i}$ where $A$ is the area of the loop.

In fact, we can take this one step further and define a new term called the magnetic dipole moment, which is defined as: $\vec{\mu }=IA\hat{n}$ where $\hat{n}$ is a vector that’s perpendicular to the plane of the loop. The direction of $\hat{n}$ is determined by the right hand rule, by curling your fingers in the direction of the current flow.

If a wire loop contains $N$ turns of wire about the same shape, simply multiply the $\vec{\mu }$ by $N$, giving you the new formula: $\vec{\mu }=NIA\hat{n}$ Now, with the power of the magnetic dipole moment, we can simply write the torque on a current loop due to a uniform magnetic field as: $\vec{\tau }=\vec{\mu }\times \vec{B}$

NOTE: This equation holds for a current loop in a two dimensional plane of arbitrary shape ONLY!

We can also extrapolate this to potential energy for energy calculations. The potential energy of a magnetic dipole is: $U=-\vec{\mu }\times \vec{B}$

Applications of Magnetic Forces

Mass Spectroscopy

The mass spectrometer separates ions according to their charge to mass ratios. 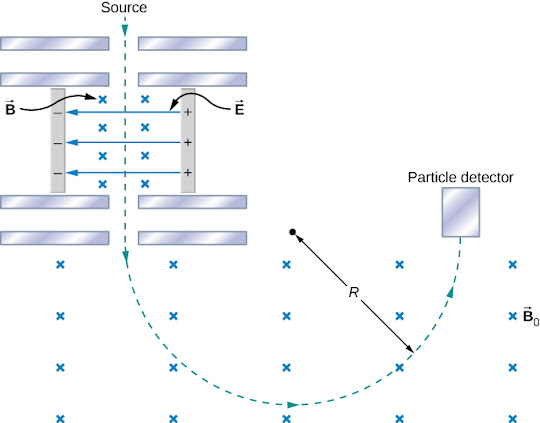In the initial stage, the magnetic field and the electric field is balanced such that any ion that doesn’t match the desired characteristics will not make it past the opening (due to being deflected into the walls)

The ions then enter a magnetic field where they travel in an arc and hit a particle detector. With this information we can determine the radius of the arc, and using the equations we’ve learned, we can use the following formula: $\frac{q}{m}=\frac{E}{B{B}_{0}R}$ If we know the charge on the ion, we can easily determine the mass, as all other variables are experimentally controlled. With this method, masses can be confirmed to one part in $10^8$.

Cyclotrons

A cyclotron uses electromagnetic fields to accelerate particles to extremely large kinetic energies.

When a positive particle is first injected into the gap, it rushes towards the negative plate (called a dee), and gains speed, when it reaches the other plate, it is only influenced by the magnetic field between the upper and lower electromagnets, giving it a uniform and known circular orbit. This gives us a known period, so when the particle reaches the gap again, we can switch the polarity of the plates, again causing the particle to be accelerated out of the gap. This process repeats itself, with the particle getting a larger and larger orbit until finally, it exits the cyclotron.

There are a couple relevant equations for the cyclotron. After the gap, the particle moves with a defined radius: $r=\frac{mv}{qB}$ and with a period of: $T=\frac{2\pi m}{qB}$

Assuming that the maximum orbital radius in the cyclotron is R, we use the equation for the period and the equation $2\pi R/v=T$. This gives us an equation for the maximum speed given by the cyclotron: $v_{max}=\frac{qBR}{m}$ This lets us further calculate the kinetic energy of the particle when ejected: $\frac{1}{2}m{v}_{max}^2=\frac{q^2{B}^2{R}^2}{2m}$ Thus, a cyclotron lets us accelerate particles to insane speed and energies, almost 30MeV!!

---

Key Equations