Complex Analysis

Complex analysis is a mathematical tool that is used to aid in the solution of mathematical and physics equations. It is very commonly used in electrical engineering due to the abundance of sin functions and oscillations.

Complex analysis heavily makes use of the complex number $i$ (we will use $j$ to avoid confusion with current) in conjunction with Euler’s formula: $e^{j\theta }=\cos \theta +j\sin \theta$ Using complex analysis can simplify computations from exponentials and sinusoids into simple algebraic calculations.

NOTE: When you have imaginary numbers in calculations, there are additional rules that you must follow. FOR EXAMPLE: YOU CANNOT COMBINE TWO SQUARE ROOTS IF ONE IS IMAGINARY.

Representing Complex Numbers

Numerical

A complex number usually consists of two parts: The real and imaginary part. For the rest of this section, we will define a general complex number: $z=x+jy$ There are a few functions that we use to extract information from complex numbers:

1. $Re(z)=x$
2. $Im(z)=y$
3. $||z||=\sqrt{x^2+y^2}$
4. $\theta ={\tan }^{-1}\frac{Im(z)}{Re(z)}$

Euler’s formula is also a very critical part of Complex Analysis. $e^{j\theta }=\cos \theta +j\sin \theta$ Using Euler’s formula, we can take any complex number z, and rewrite it as:

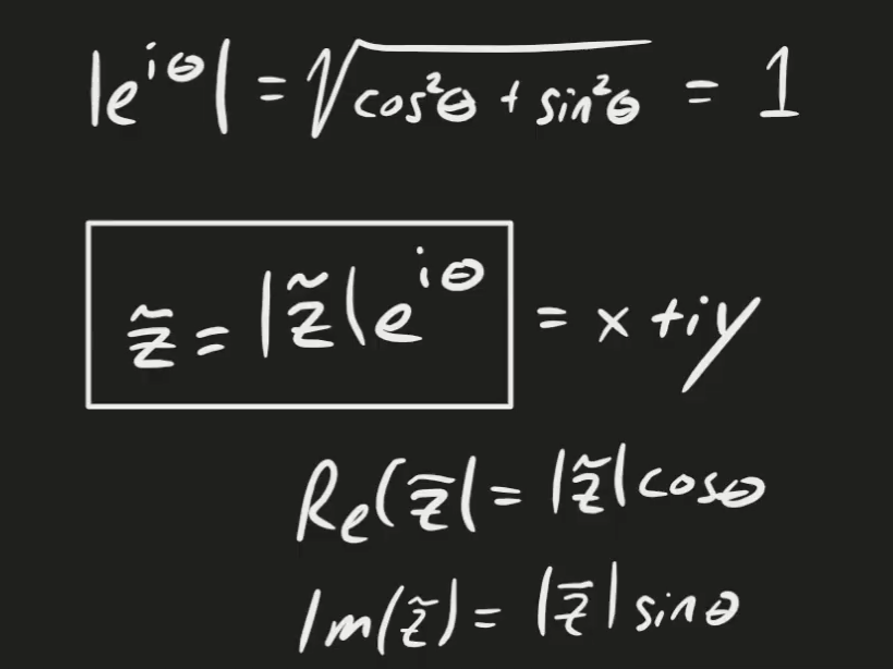
Graphical

Imaginary numbers can be represented on the coordinate plane, with the real component on the x axis, and the imaginary portion on the y axis!

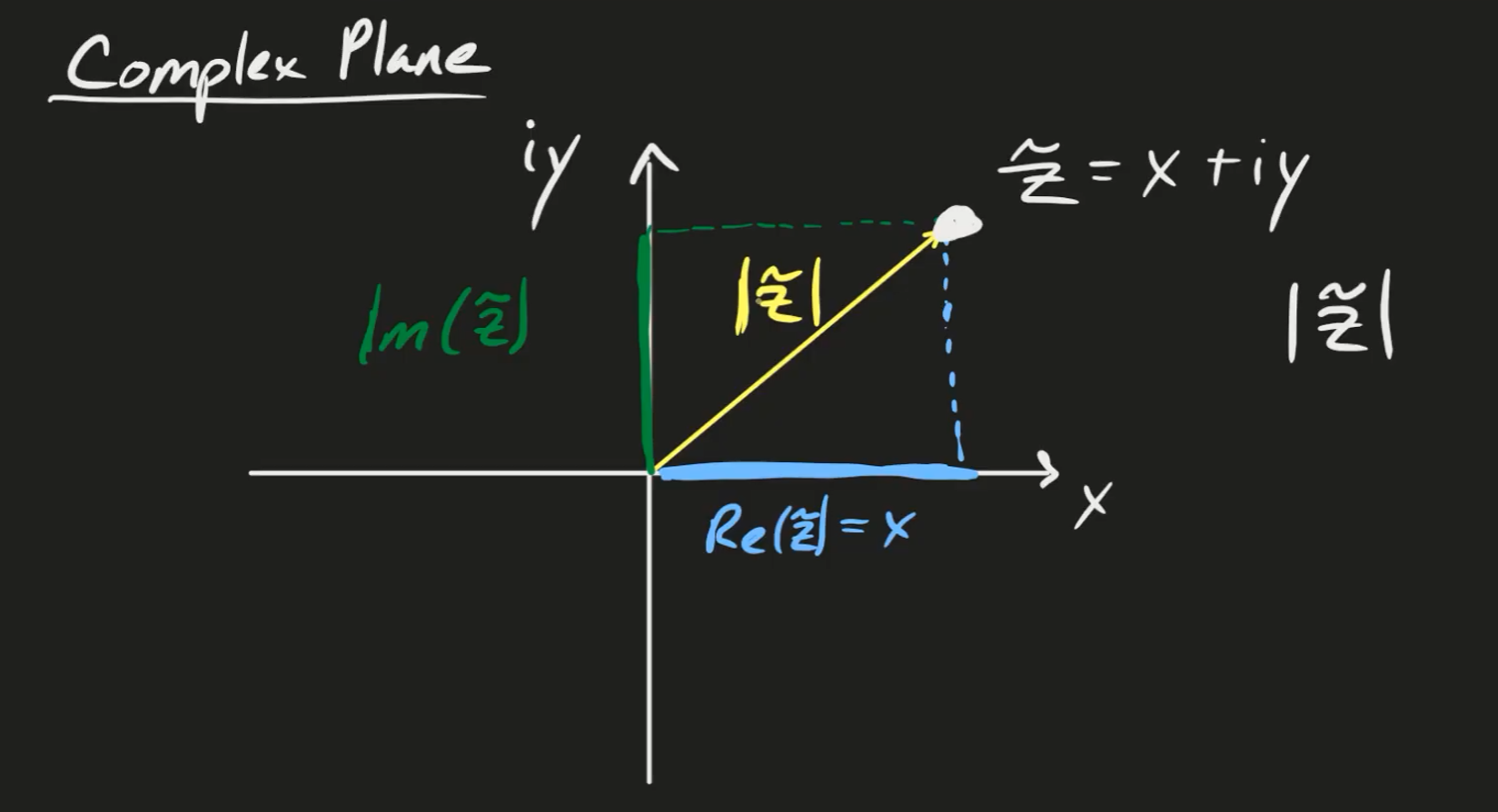
We can also represent complex numbers graphically with polar coordinates. By using Euler’s formula, we can represent a complex number as an angle and a magnitude.

Applying Complex Analysis to Physics/Electrical Engineering:

When used in Physics or Electrical Engineering, we convert from real to complex numbers, execute our computations, and then convert back to real numbers.

We cannot use Ohm’s Law in AC circuits, it simply doesn’t work. However, we can define a new quantity called the reactance. The reactance is used in place of resistance in AC circuits to compute results and the reactance can be used with Ohm’s law to solve circuits.

Resistors

Resistors in AC can be modelled as such: To find the real result, we simply take the cosine of the magnitude (the capital letters).

The reactance of a resistor is simply $X_R=R$

Inductors

The reactance of an inductor

Capacitors

Putting it All Together

Now that we have our complex representations or reactance of these components, we can use complex analysis to greatly simplify problems with AC! Complex analysis allows us to draw an analogous system to Ohm’s Law. Instead of using the resistance, we combine the reactance of all the components and find the magnitude of the complex number in order to find the impedance of the circuit. $||z||=\sqrt{Re(z{)}^2+Im(z{)}^2}$ We can take this number and multiply it by the current to get voltage, or divide the voltage by the impedance to get the current (depends on what the problem gives you).