Inductance

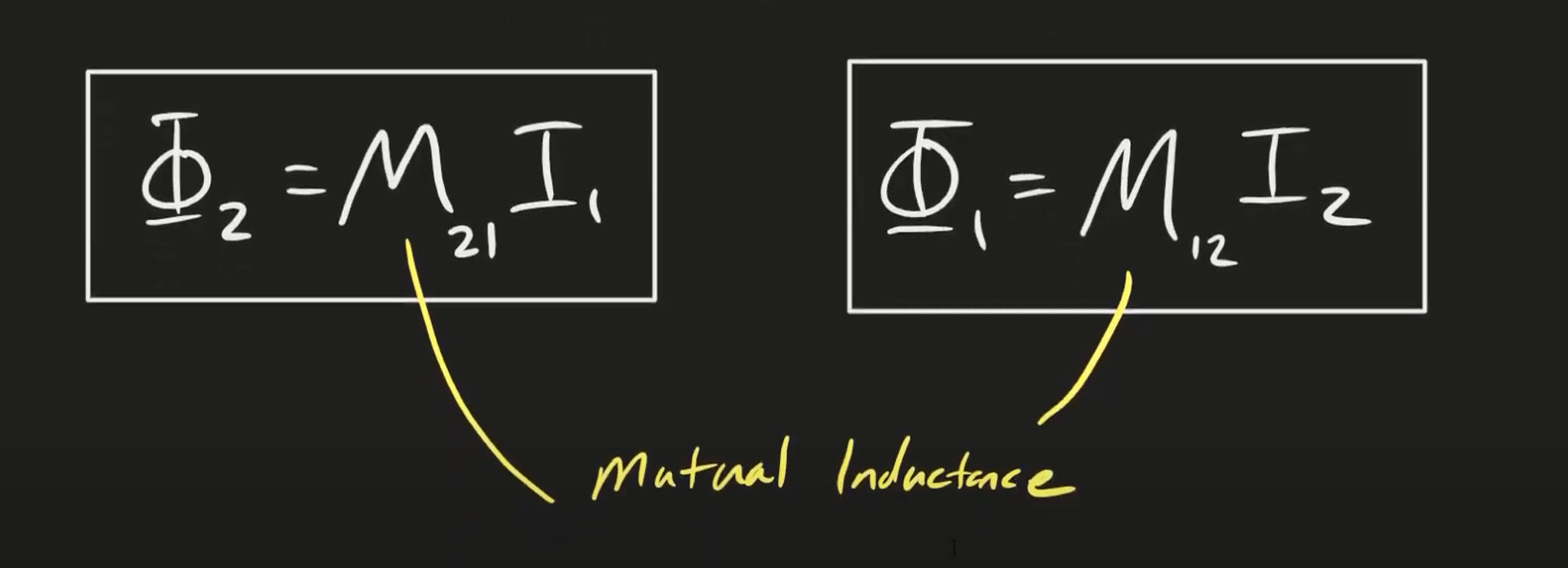
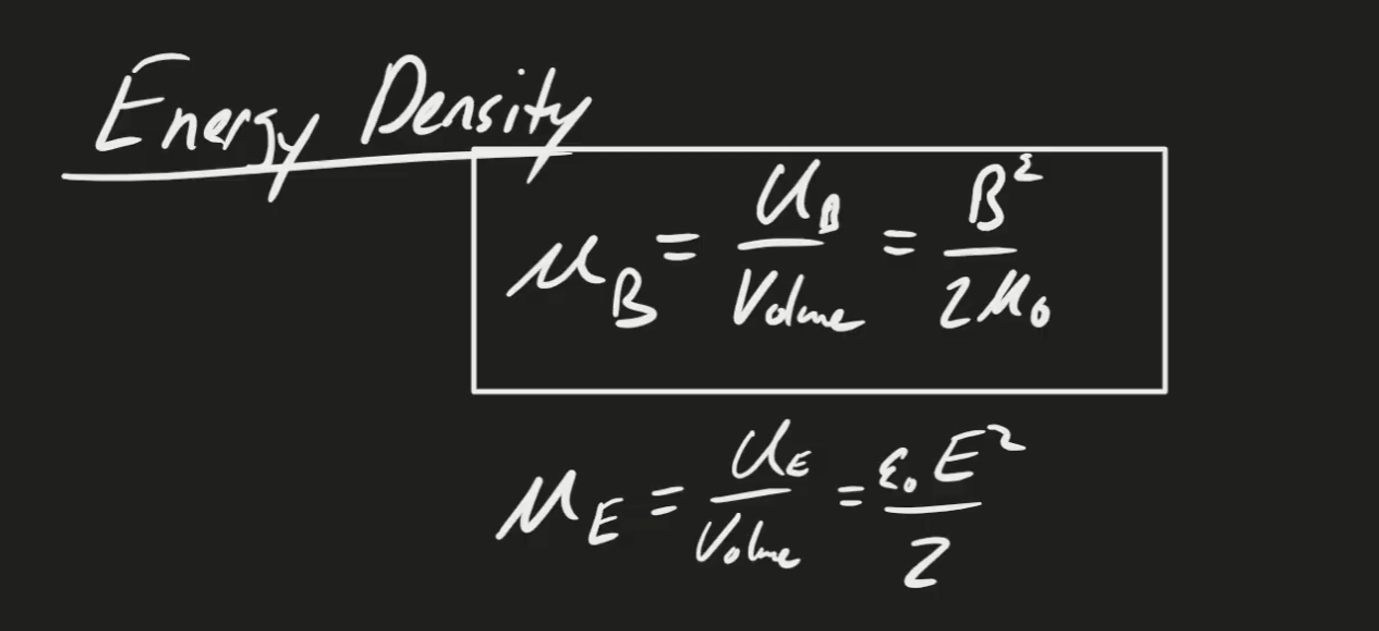Mutual Inductance:

If we have two loops right next to each other, we know from our study of Faraday’s Law and Biot-Savart Law that one loop with current will create a magnetic field that will influence and create a current in loop two. Examining the equations, we can tell that he flux and the current are proportional to current. From this, we can define a new property called mutual inductance: There is a way to calculate the value of the mutual inductance (in units of Henrys (H)). This formula has the following properties:

1. Solely geometric (the electrical properties of the loops have no influence) and really complicated to solve.
2. $M_{21}=M_{12}$ are exactly the same. Thus we drop the subscript and usually call it just $M$.

The mutual inductance of coil 2 with respect to coil 1 is given by the below equation. ${\Phi }_{21}$ should be interpreted as the flux through loop 2 caused by the magnetic field from loop 1. $M=\frac{N_2{\Phi }_{21}}{I_1}$and similarly: $M=\frac{N_2{\Phi }_{12}}{I_2}$ The value of M can be found theoretically or experimentally. But once you have M, you can easily find flux in both loops with the current in each loop.

For Faraday’s Law we do not care about $\Phi$ but rather $-\frac{d\Phi }{dt}$. Thus, we can now rewrite Faraday’s Law in terms of the mutual inductance: ${\mathcal{E}}_1=-\frac{d{\Phi }_1}{dt}=-M\frac{d{I}_2}{dt}$ or ${\mathcal{E}}_2=-\frac{d{\Phi }_2}{dt}=-M\frac{d{I}_1}{dt}$

Practice Problem:

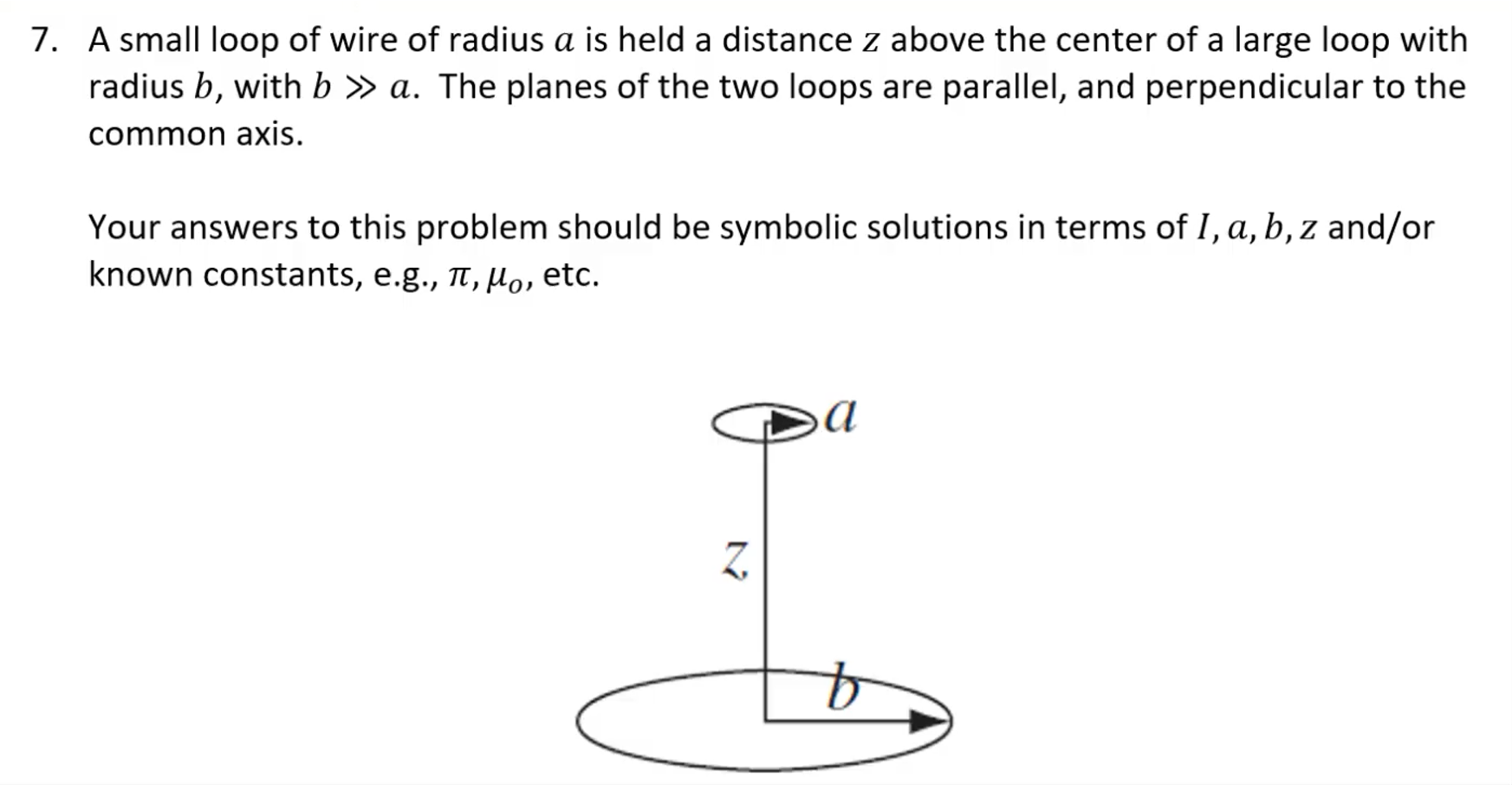
Suppose a Current I flows in the big loop. Find the flux through the little loop. (The little loop is so small that you may consider the field of the big loop to be essentially constant across the little loop that lies on the axis above the large loop).

To solve this question, we must look back to Biot-Savart Law to find the magnetic field above the large loop on the z axis. 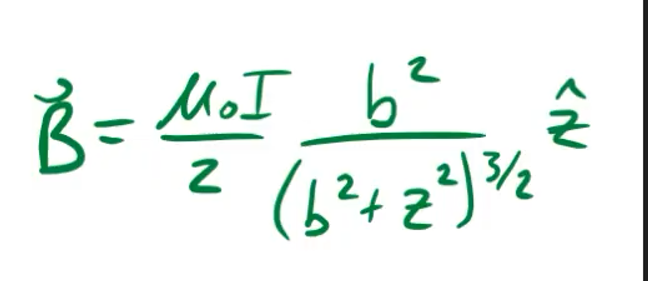The flux through the loop can be given through Faraday’s Law: $\mathcal{E}=\oint \vec{B}\cdot \overrightarrow{dA}=BA$ Substituting in values for $B$ and $A$, we arrive at the following solution:

What is the mutual Inductance $M_{ab}$ defined by $\Phi =M_{ab}{I}_b$?

To solve this, we simply take our previous answer in part a and divide by I, the current in loop b.

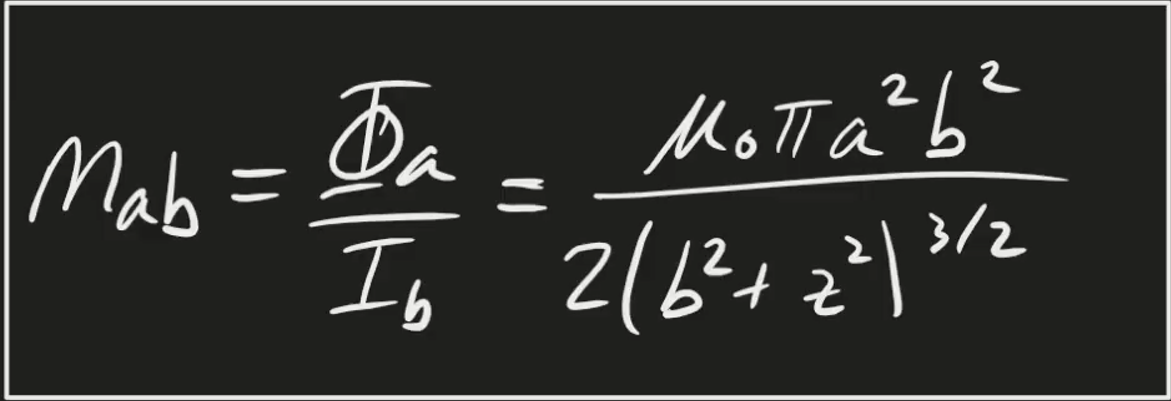
Suppose we induce a current I in loop a, what is the flux in loop b?

This question may be tricky upon first glance, but using what we’ve learned, it becomes easy. At first, it may seem that the field from loop A passing through loop B is complicated, but by using the property of mutual inductance above, we know that: ${\Phi }_b=M{I}_a$

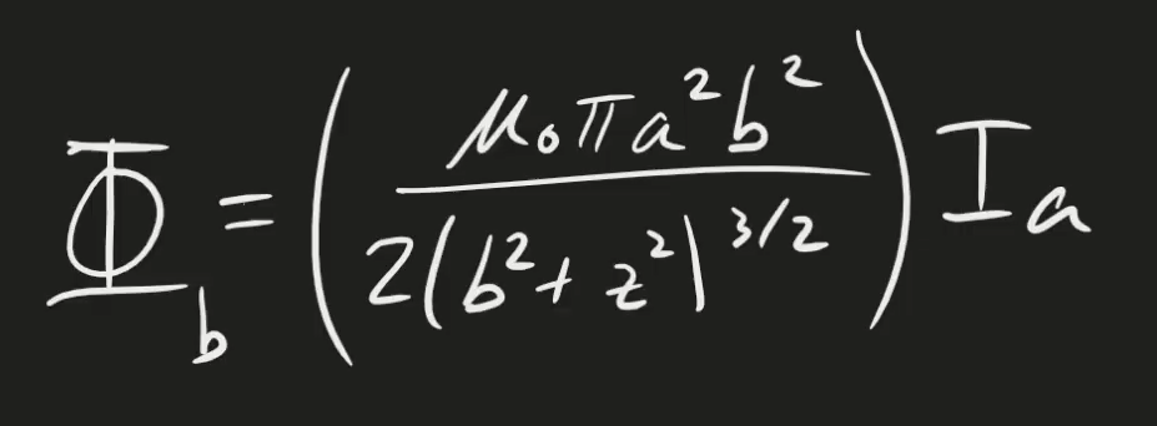
Self-Inductance:

A single loop with current I, will create its own magnetic field. Its own magnetic field will penetrate its own area and create its own flux. We assign a new term for the Self-Inductance called $L$ (also measured in Henries “H”): $N{\Phi }_m=LI$ We can again use Faraday’s Law to rewrite the induced EMF in terms of the self-inductance: ${\mathcal{E}}_{ind}=-L\frac{dI}{dt}$

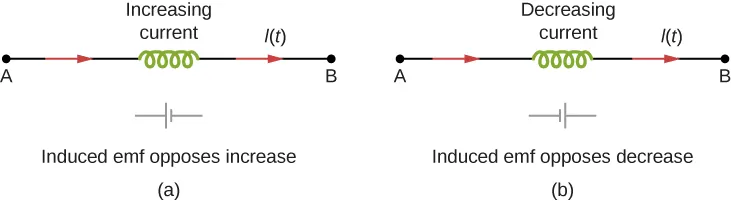
NOTE: To determine the sign of L, it is best to ignore the signs of E and dI/dt and simply take the absolute value, as L is always positive!

An inductor is a circuit element that purposefully provides a lot of self inductance. Just as predicted by Lenz’s law, the induced EMF across an inductor always works to oppose the change in current (and thus the change in magnetic fields).

Self Inductance of a Cylindrical Solenoid:

Consider a long, cylindrical solenoid with length l, cross-sectional area A, and N turns of wire. We assume that the length of the solenoid is so much larger than its diameter that we can take the magnetic field to be $B={\mu }_{0}nl$ throughout the interior of the solenoid, that is, we ignore end effects in the solenoid. With a current I flowing through the coils, the magnetic field produced within the solenoid is: $B={\mu }_0\frac{N}{l}I$ The flux ends up being: $BA=\frac{{\mu }_{0}NA}{l}I$ We then plug this in to the equation given above for the inductance: $L_{solenoid}=\frac{N{\Phi }_m}{I}=\frac{{\mu }_0{N}^{2}A}{l}$

NOTE: IT IS VERY IMPORTANT TO NOTICE THAT WE MULTIPLY BY N TWICE!!! YOU MUST DO THIS WHEN FINDING THE SELF INDUCTANCE, SO BE SURE TO FOLLOW THE FORMULA TO A T!

Multiplying by $l/l$, simplifying $N/l$ to $n$ (turns per meter) and changing $A\ast l$ to $V$, we arrive at the simple solution: $L={\mu }_0{n}^{2}V$

Self Inductance for a Rectangular Toroid:

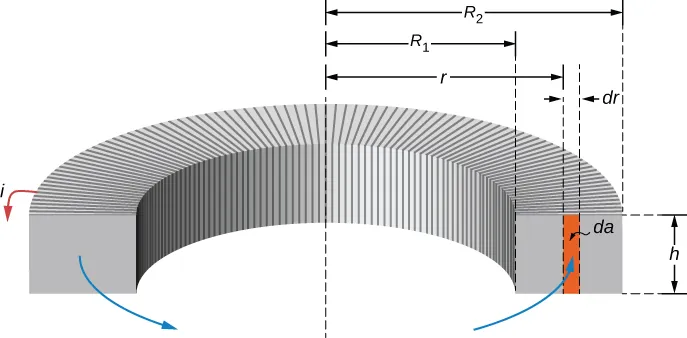To calculate the self-inductance of the rectangular toroid below, we follow a similar process, but slightly more complicated this time.

The magnetic field inside a toroid is given by (r is distance from central axis of the toroid): $B=\frac{{\mu }_{0}NI}{2\pi r}$ Because the field changes within the toroid, we must calculate the flux by integrating over the toroid’s cross-section. We use the infinitesimal cross section area of $da=hdr$ and obtain: ${\int }_{R_1}^{R_2}\frac{{\mu }_{0}NI}{2\pi r}\ast hdr$ This becomes: $\frac{{\mu }_{0}NhI}{2\pi }\ast \ln \frac{R_2}{R_1}$ And from the self inductance equation, we finally get the self-inductance of a rectangular toroid: $L=\frac{{\mu }_0{N}^{2}h}{2\pi }\ast \ln \frac{R_2}{R_1}$

Energy in Magnetic Field (Inductors)

The energy in any inductor is given by the equation: $U=\frac{1}{2}L{I}^2$ and is given when you take the volume integral over the magnetic energy density: $u_{total}=\frac{1}{2{\mu }_0}\iiint B^{2}dV$

This computation can be difficult, so we sometimes think of this in terms of the energy density: