Ampere's Law

Ampere’s Law gives us a way to find Magnetic Forces and Fields without using the Biot-Savart Law. It is particularly useful in cases of symmetry between $\vec{B}$ the electric field and $\overrightarrow{dl}$. The law itself bears many similarities to Gauss’ Law

Ampere’s Law is as follows: $\oint \vec{B}\cdot \overrightarrow{dl}={\mu }_0{I}_{encl}$ $I_{encl}$ is the total current passing through the open surface whose perimeter is the path of integration. To figure out if $I_{encl}$ is negative or positive, curl your right hand in the direction of the path of integration. If I passes through the surface in the same direction as your extended thumb, I is positive; if I passes through the surface in the direction opposite to your extended thumb, it is negative. YOU MUST DO THIS! Otherwise, you may get the negative of the correct answer.

NOTE: The advantage of using this law is to be able to pull B out of the equation. If you cannot achieve that with an Ampere shape, it is likely that Ampere's Law is not the ideal method to solve the problem!

WARNING: dl DOES NOT represent the same thing as it does in Biot-Savart! It instead represents a length element ON THE AMPERE CURVE. In Biot-Savart it represents a length element on the current carrying wire.

Examples and Strategies

Thin Wires:

In order to solve this problem, we notice that the field is always the same in a circle around the wire. We further notice the obvious symmetry between the field and the current. Using these two observations, we can deduce a few things:

1. $\vec{B}$ is constant and can be pulled out of the line integral.
2. $\vec{B}$ is always parallel to $\overrightarrow{dl}$

Using these two deductions and the fact that the line integral of a circle is the circumference, we arrive at the following result: $B=\frac{{\mu }_{0}I}{2\pi r}$ This is the same result we got using the Biot-Savart Law.

Thick Wire (QUIZ QUESTION):

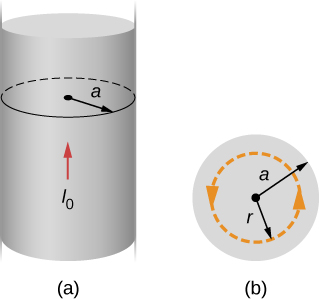
This problem has the same setup as the thin wire, but differs in a key way. In this example, the magnetic field inside the wire varies, since the $I_{encl}$ grows larger as the radius inside grows.

To determine the $I_{encl}$ at all points inside the wire, we will have to use a concept called Current Density. The current density is much like the charge density, but varies in a key way. Because current is already a 1 dimensional thing, we only need to divide by the area the current occupies to find the current density! The formula for UNIFORM current density is given by: $J=\frac{I_{total}}{A_{total}}$ $A_{total}$ in this example is simply the area of the circle: $\pi a^2$ (a is the maximum radius of the wire. Thus, in this example, J is simply $\frac{I_0}{\pi a^2}$. To find the current inside the wire at any point, we simply do the following: $I_{encl}={\int }_0^{r}J\cdot dA$

1. For $r<a$, $I_{encl}$ is simply $J\pi r^2$.
2. Outside, the $I_{encl}$ is simply $I_0$ (the value of the above integral when $r=a$).

Using all this information and the fact that the LHS is simply the same as before ($2\pi r$), we find two solutions in our solution set:

1. For $r\le a$, $B=\frac{{\mu }_0{I}_{0}r}{2\pi a^2}$

2. For $r\ge a$, $B=\frac{{\mu }_0{I}_0}{2\pi r}$ Case 2 is the exact same result that we found in the thin wire example above.

   NOTE: At the boundary of the two solutions, either solution is valid and both solutions will give you the same answer. This is an easy way to check if you answer is correct.