Chapter 6 - Maxwell's Equations for Time-Varying Fields

Now that we’ve considered static conditions for both the electric and magnetic fields, it’s time to consider the dynamic conditions when those fields vary!

Faraday’s Law

Michael Faraday hypothesized that if a current could create a magnetic field, then the opposite should be true. A magnetic field must be able to create a current. Chasing this lead, he eventually found that a change in magnetic field would cause a current. This is illustrated in Faraday’s Law: $V_{emf}=-N\frac{d\Phi }{dt}$ From this equation and the equation for magnetic flux $\Phi$, we can see that there are three avenues for $V_{emf}$ to be generated:

1. A time varying magnetic field produces a transformer EMF $V_{emf}^{tr}$
2. A moving loop with time varying area in a static B field produces a motional EMF $V_{EMF}^m$
3. A moving loop in a time varying field

Stationary Loop in Time Varying Field

Due to the only time-varying component being the B field, Faraday’s Law breaks down to: $V_{emf}=-N{\int }_S\frac{\partial B}{\partial t}\cdot ds$

IMPORTANT

The direction of the EMF is governed by Lenz’s Law, which dictates that the emf produced will always oppose the change in the magnetic field.

The ideal transformer is a direct application of Faraday’s Law for time-varying magnetic fields. The ideal transformer routes the flux from one inductive coil through to another. You can derive the following equations:

• $\frac{V_1}{V_2}=\frac{N_1}{N_2}$
• $\frac{I_1}{I_2}=\frac{N_2}{N_1}$
• $Z_{in}=(\frac{N_1}{N_2}{)}^2\cdot Z_L$

Moving Conductor in a Static Magnetic Field

Consider a wire of length l moving across a static magnetic field $\vec{B}=B_0\hat{z}$ and velocity $\vec{u}$. The force on a particle due with charge q due to the motion in a magnetic field: ${\vec{F}}_m=q(\vec{u}\times \vec{B})$ This magnetic force is exactly equal to the electrical force that’s exerted on the particle by the electric field ${\vec{E}}_m$. This is called a motional electric field: ${\vec{E}}_m=\frac{{\vec{F}}_m}{q}=\vec{u}\times \vec{B}$ This motional EMF is in the direction perpendicular to the plane containing u and B. Follow the right hand rule. With the motional EMF, we can solve for the $V_{emf}$ in the wire: $V_{emf}=\int {\vec{E}}_m\cdot dl=\int (\vec{u}\times \vec{B})\cdot dl$

For the case of a conducting wire, we simply find that: $V=-u{B}_{0}l$ Of course, you could have also solved this problem using the general formula for Faraday’s law, carrying through the complete integral. However, you must consider the area to be the area drawn by the wire as it moves through space. I personally prefer the full Faraday’s solution, as it can more effectively handle general cases.

The Electromagnetic Generator

Electromagnetic generators drive spinning loops in magnetic fields in order to produce $V_{emf}$ and consequently, electrical power. If we start from the standard Faraday’s Law equation, we can formulate the following equation given a field $B_0$, loop area A, and angular velocity $\omega$: $\Phi ={\int }_S\vec{B}\cdot ds={\int }_S\hat{z}{B}_0\cdot \hat{n}ds=B_{0}A\cos (\alpha +C_0)$ ,which gives the following EMF: $V_{emf}=-\frac{d\Phi }{dt}=A\omega B_0\sin (\omega t+C_0)$

Moving Conductor in a Time-Varying Magnetic Field

If we encounter problems where both the magnetic field and the geometry are changing, we must proceed with the full form of Faraday’s Law.

Displacement Current

Ampere’s Law in differential form is given as: $\nabla \times \vec{H}=\vec{J}+\frac{\partial \vec{D}}{\partial t}$ If we integrate this over an arbitrary open surface S, with contour C, and apply Stokes theorem, we get the following: $\oint H\cdot dl=I_c+{\int }_S\frac{\partial D}{\partial t}\cdot ds$ $I_c$ is the conduction current, the current flowing into the surface S, but what is the term on the right? We call this the displacement current! $I_d={\int }_S\frac{\partial D}{\partial t}\cdot ds={\int }_S{\vec{J}}_d\cdot ds$ The displacement current doesn’t transport free charges, but it behaves like a real current. It comes up most famously in a parallel plate capacitor, and illustrates that the magnetic field between the plates of the capacitor is still the same as in the wires connecting the capacitor. In most cases, we neglect the displacement current, since in a perfect conductor, $D=E=0$. (Note: $E=\frac{I_c}{\sigma A}$)

Boundary Conditions for Electromagnetics

Even when considering the dual case of electromagnetics, the boundary conditions derived in static cases remain the same. These are summarized in the following table

Charge-Current Continuity Relation

Under static conditions, the charge density ${\rho }_v$ and the current density $\vec{J}$ are totally independent of one another. This assumption falls flat if we no longer assume conditions are static. If we draw an arbitrary boundary around a region of space with some charge $Q$, we can obviously see that in order for charge to decrease, there must be net flow outwards. For charge in the volume to increase, we must have net flow inwards! We can formulate this with the following equation: ${\oint }_S\vec{J}\cdot ds=-\frac{d}{dt}{\int }_V{\rho }_{v}dV$ We can apply the divergence theorem and simplify to arrive at the charge-current continuity relation: $\nabla \cdot \vec{J}=-\frac{\partial {\rho }_v}{\partial t}$ If we assume that the charge is not changing ($\frac{\partial {\rho }_v}{\partial t}=0$), then we arrive at Kirchhoff’s Law: ${\oint }_S\vec{J}\cdot ds=0$

Electromagnetic Potentials

Since electric and magnetic fields are linked, it’s a no brainer to explore the relationship between the electrical scalar potential V and the magnetic vector potential A. In the dynamic case, Faraday’s Law becomes: $\nabla \times \vec{E}=-\frac{\partial \vec{B}}{\partial t}$ Due to the relation $B=\nabla \times A$, we can express this as: $\nabla \times \vec{E}=-\frac{\partial }{\partial t}(\nabla \times \vec{A})$ Further substitutions and simplification leads to the following equation: $\vec{E}=-\nabla V-\frac{\partial \vec{A}}{\partial t}$

This has implications. In the case of a charge distribution, we might be tempted to simply write the V as a function of time, but we haven’t considered the influence of the magnetic field. The magnetic field, much like an inductor in a circuit, doesn’t permit the voltage to jump! Thus, we rewrite the voltage as follows: $V(R,t)=\frac{1}{4\pi ϵ}{\int }_{V^{\prime }}\frac{{\rho }_v(R_i,t-R^{\prime }/u_p)}{R^{\prime }}d{V}^{\prime }$ In this equation, $V(R,t)$ is called the retarded scalar potential. The retarded vector potential is also defined: $A(R,t)=\frac{\mu }{4\pi }{\int }_{V^{\prime }}\frac{J(R,(R_i,t-R^{\prime }/u_p))}{R^{\prime }}d{V}^{\prime }$ Using phasor analysis, we can analyze these two equations in tandem. Take an arbitrary phasor time delayed by the retarded potential. ${\rho }_v(R_i,t-R^{\prime }/u_p)=\Re [{\rho }_v(R_i)e^{-jk{R}^{\prime }}{e}^{j\omega t}]$ , where $k=\frac{\omega }{u_p}$. With that, we obtain the following two expressions:

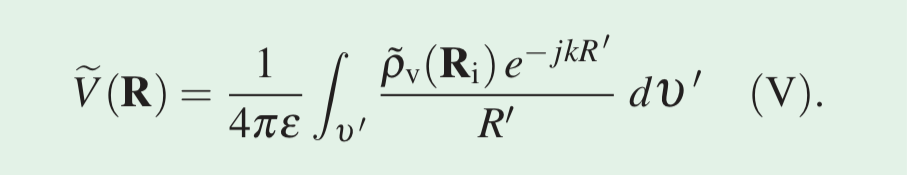
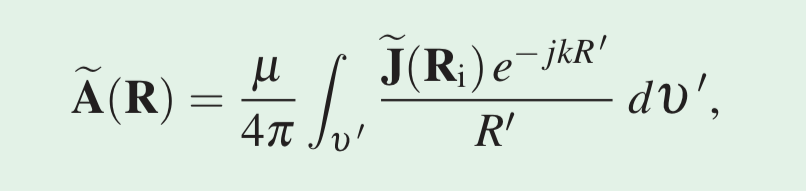
This means that, given a time harmonic current density distribution with a phasor J, we can use the following equation to successively determine both $E$ and $H$: $\nabla \times \tilde{E}=-j\omega \mu \tilde{H}$or $\tilde{H}=-\frac{1}{j\omega \mu }\nabla \times E$